Um dia...

Um dia eu vi um tiroteio. Mas, entre mortos e feridos, salvaram-se todos.
Um dia eu vi um homem tentar se jogar daquele viaduto ali pertinho da passarela 11. Mas, felizmente, os bombeiros chegaram a tempo.
Um dia eu vi um outro homem cair no vão entre o trem e a plataforma. Mas, por sorte, foram apenas algumas escoriações.
Um dia eu vi você olhar pra mim. Eu. Eu olhar. Eu olhar você. Mas já era tarde demais. Ou, quem sabe, cedo de menos

http://bacaninha.uol.com.br/v1/#

Numerais cardinais. Qual foi a sua classificação no exame ?

Qual foi a sua classificação no exame

vestibular, meu filho?

- iiii, pai! eu fiquei em 2853º. Como é que se

fala isso, mesmo??

Veja como se devem pronunciar os numerais

cardinais:

1º = primeiro

2º = segundo

3º = terceiro

4º = quarto

5º = quinto

6º = sexto

7º = sétimo

8º = oitavo

9º = nono

10º = décimo

20º = vigésimo

30º = trigésimo

40º = quadragésimo

50º = quinquagésimo

60º = sexagésimo

70º = septuagésimo

80º = octogésimo

90º = nonagésimo

100º = centésimo

200º = ducentésimo

300º = trecentésimo

400º = quadringentésimo

500º = quingentésimo

600º = seiscentésimo ou sexcentésimo

700º = septingentésimo

800º = octingentésimo

900º = nongentésimo ou noningentésimo

1000º = milésimo

de 2000 em diante, lê-se facultativamente o

milésimo como cardinal ou

como ordinal, ou seja, lê-se o dois milésimo ou

o segundo

milésimo.

Agora é só juntar tudo, como, por exemplo:

14596º = o quatorze milésimo quingentésimo

nonagésimo sexto ou o

décimo quarto milésimo quingentésimo nonagésimo

sexto.

A resposta do vestibulando, então, deve ser

esta:

- iiii, pai! eu fiquei em dois (ou segundo)

milésimo octingentésimo

quinquagésimo terceiro lugar.

Para uma fácil aceitação da população nordestina, os cinemas locais mudam os nomes dos filmes. Veja abaixo o nome de alguns filmes que já foram mudados pelos nordestinos.

Uma Linda Mulher
A Cabrita Aprumada

O PoderosoChefão
O Coroné Arretado

O Exorcista
Arreda Capeta!

Os Sete Samurais
Os Jagunço di Zóio Rasgado

Godzila
O Calangão

Os Brutos Também Amam
Os Vaquero Baitola

Sansão e Dalila
O Cabiludo e a Quenga

Perfume de Mulher
Cherim di Cabocla Tora, Tora, Tora! Oxente, Oxente, Oxente!

Mamãe faz cem anos
Mainha num Morre Mais!

Guerra nas Estrelas
Arranca-rabo nu Céu

Um Peixe Chamado Wanda
O Lambarí cum nomi di Muié

Noviça Rebelde
Beata Increnquera

O Corcunda de Notre Dame
O Monstrim da Igreja Grandi

O Fim dos Dias
Nóis Tamo é Lascado

Um Cidadão Acima de Qualquer Suspeita
Um Cabra Pai D' égua di Quem Ninguém Discunfia

Os Filhos do Silêncio
Os Minino du Mudim

A Pantera Cor-de-rosa
A Onça Aviadada bjim kkkk.....

Dicas para blog...

http://www.dicasparablogs.com.br/2009/03/melhor-site-de-musica-para-colocar-no_05.html

20 perguntas interessantes

1-Por que é que as viúvas negras e as fêmeas do louva-deus matam os machos depois do acasalamento?
R:Para impedir a sessão de roncos que se segue.

2-Por que é que os homens não têm a crise da meia idade?
R:Porque ficam todos parados na adolescência.

3-Qual a diferença entre ir a um bar sozinha e ir a um circo?
R:Quando você vai ao circo os palhaços não falam contigo.

4-Por que é que os homens gostam de mulheres inteligentes?
R:Porque os opostos atraem-se.

5-Qual o livro mais fino do mundo?
R:"O que os homens sabem sobre as mulheres".

6-O que os homens geralmente entendem como "preliminares" para sexo?
R:Meia hora implorando para ir para a cama com eles.

7-Como se pode ver que um homem está sexualmente excitado?
R:Se ele estiver respirando.

8-Qual a diferença entre os homens e a fruta?
R:É que a fruta amadurece um dia...

9-Qual a semelhança entre os dinossauros e os homens inteligentes?
R:Ambos estão extintos.

10-Por que é que as pilhas são melhores que os homens?
R:Porque as pilhas têm pelo menos um lado positivo.

11-O que você deve dar a um homem que pensa que tem tudo?
R:Uma mulher pra ensiná-lo como funciona.

12-Por que os homens querem casar com virgens?
R:Eles não suportam críticas.

13-Como se chama um homem interessante no Brasil?
R:Turista.

14-Quantos homens são necessários pra fazer pipoca?
R:Três. Um pra segurar a panela e os outros pra fazerem papel de machos e balançar o fogão.

15-O que têm em comum o clitóris, os aniversários e a tampa do vaso sanitário?
R:Os homens sempre erram.

16-Por que muitas mulheres fingem o orgasmo?
R:Porque muitos homens fingem as preliminares.

17-Por que os homens não costumam mostrar seus sentimentos verdadeiros?
R:Porque eles não têm nenhum.

18-Por que apenas 10% dos homens vai para o céu?
R:Porque se todos fossem, seria o inferno!

19-Qual a diferença entre homens e porcos?
R:Porcos não viram homens quando bebem.

20-Por que os homens são como as pipocas?
R:Eles te satisfazem, mas por pouco tempo.

As diabruras dos números interessantes

Dizem os seguidores de Pitágoras que todos os números (inteiros) são interessantes. Para aceitar essa verdade dogmática seria preciso conceituar bem o que é que nos permite denominar um número de interessante.

Mesmo que não cheguemos a um acordo sobre isso, parece aceitável que alguns números sejam, de fato, interessantes. Veja, por exemplo, o número 142 857. Aparentemente é apenas mais número. Mas. quando multiplicado r 1,2,3,4,5 e 6, tem a particularidade de apresentar produtos com os mesmos algarismos e na mesma ordem, como se estivessem escritos num cilindro. Se o multiplicarmos por 1, 3, 2. 6, 4 e 5 teremos:
142 857 x 1 = 142 857:
142 857 x 3 = 428 571 (quando multiplicado por 3 o resultado é um número com os mesmos algarismos, com o 1 passando para o final);
142 857 x 2 = 285 714 (o resultado é um numero com os mesmos algarismos, com o l e o 4 passando para o final);
142 857 x 6 = 857 142 ( vê-se que o 1, o 4 e o 2 passam para o final);
142 857 x 4 = 571 428 (o resultado mostra que 1,4,2 e 8 passam para o final);
142 857 x 5 =714 285 (de novo, um produto com os mesmos algarismos: 1,4,2,8 e 5 vão para o final).

Esses exemplos servem para mostrar que o número 142 857 possui a propriedade de, quando multiplicado por qualquer número de 1 a 6, resultar em outro número com os mesmos algarismos e na mesma ordem cíclica. Vários livros de curiosidades matemáticas têm dado atenção ao 142857. 0 professor Mello e Souza, conhecido pelo nome de Malba Tahan, em seu livro Diabruras da Matemática, já destacava, em 1943, o comportamento desse número quando multiplicado por 7 e por 8:
142 857x7 = 999 999
142 857 x 8 = 1 142 856 (note que os algarismos são os mesmos, à exceção do 7 que se transformou no 1 inicial e no 6 final). Você poderá descobrir mais propriedades interessantes desse número, basta efetuar algumas multiplicações e observar atentamente. Vamos tentar encontrar a representação decimal da fração 1/7 (dividindo o 1 pelo 7) 1/7 = 0,142 857 142857 142857...

Repare que obtivemos uma dízima periódica simples, cujo período é o nosso já conhecido 142 857. Com isso fica fácil prever o que ocorreria com as frações 3/7, 2/7, 6/7, 4/7 e 5/7. Mesmo que você não seja um maníaco por números, não há como não se render ao curioso 142 857. Como ele, existem outros que até causaram certa polêmica, quanto a serem ou não interessantes, como o número 1 729. Conta-se que, certa vez, o matemático inglês G. H. Hardy foi visitar o matemático indiano Ramanujan, que era seu discípulo. Hardy relatou ao indiano que viera num táxi de número 1729, que ele considerava um número sem importância. Ramanujan, então, discordou: "Absolutamente não; 1 729 é um número muito interessante, pois é o menor número que pode ser expresso pela soma de dois cubos de duas maneiras distintas: 93 + 103 = 1 729 ou l3 + 123 = 1 729".

Ainda que você não tenha esse entusiasmo pelos números, há de concordar que existem números interessantes e, conseqüentemente, aceita que a família dos números possa ser dividida em duas classes: a dos interessantes e a dos não-interessantes. Esta última deve ter um número que é o menor da classe, o que faz dele um número interessante - já escrevi sobre isso em SUPERINTERESSANTE ano 6, número 2. Esses exemplos revelam idéias simples que entram na construção de raciocínios e servem, por força de sua própria simplicidade, à ciência e à arte. Pena que não se possa também classificar as aulas de nossas escolas em interessantes e não-interessantes.

Consegue resolver a equação?

Dicas para Vestibular

http://g1.globo.com/Noticias/Vestibular/0,,MUL854281-5604,00.html

40 anos do homem na lua

http://g1.globo.com/Sites/Especiais/0,,17082,00.html

Gripe suina

Mortes por novagripe no país chegam a 368, diz governo

Jogos educativos

Voce que gosta de jogos de matemática entre no sitehttp://jogoseducativos.jogosja.com/jogos-educativos-de-Matem%C3%A1tica.aspx

Guia da reforma ortográfica

Imprima o guia da reforma ortográfica (arquivo em PDF)

http://download.globo.com/vestibular/Guia_rapido_do_G1_sobre_o_acordoOrtografico.pdf

Folclore

Artigos Relacionados

Memoria

Caso você esteja muito esquecido nos estudos, entre no site

http://www.vestibular.brasilescola.com/resumos-de-livros/

Numéros Inteiros relativos

Interseção do conjunto dos naturais e dos inteiros.

Pertencem ao conjunto dos números inteiros os números negativos, os números positivos e o zero. Fazendo uma comparação entre os números naturais e os inteiros percebemos que o conjunto dos naturais está contido no conjunto dos inteiros.

N = { 0,1,2,3,4,5,6, ... }

Z = { ... , -3,-2,-1,0,1,2,3,4, ... }

N Z

O conjunto dos números inteiros é representado pela letra Z maiúscula. Os números positivos são representados com o sinal de (+) positivo na frente ou com sinal nenhum (+2 ou 2), já os números negativos são representados com o sinal de negativo (-) na sua frente (-2).

►Os números inteiros são encontrados com freqüência em nosso cotidiano, por exemplo:

♦ Exemplo 1:

Um termômetro em certa cidade que marcou 10^°C acima de zero durante o dia, à noite e na manhã seguinte o termômetro passou a marcar 3°C abaixo de zero. Qual a relação dessas temperaturas com os números inteiros?

Quando falamos acima de zero, estamos nos referindo aos números positivos e quando falamos dos números abaixo de zero estamos referindo aos números negativos.

+10° C ------------- 10° C acima de zero
- 3° C --------------- 3° C abaixo de zero

♦ Exemplo 2:

Vamos imaginar agora que uma pessoa tem R$500,00 depositados num banco e faça sucessivas retiradas:

• dos R$500,00 retira R$200,00 e fica com R$300,00

• dos R$300,00 retira R$200,00 e fica com R$100,00

• dos R$100,00 retira R$200,00 e fica devendo R$ 100,00

A última retirada fez com que a pessoa ficasse devendo dinheiro ao banco. Assim:

Dever R$100,00 significa ter R$100,00 menos que zero. Essa dívida pode ser representada por – R$100,00.

►Oposto de um número inteiro

O oposto de um número positivo é um número negativo simétrico. Por exemplo: o oposto de +2 é -2; o oposto de -3 é +3.

►O conjunto dos números inteiros possui alguns subconjuntos:

- Inteiros não – nulos
São os números inteiros, menos o zero.
Na sua representação devemos colocar * ao lado do Z.
Z* = {..., -3, -2, -1, 1, 2, 3,...}

- Inteiros não positivos
São os números negativos incluindo o zero.
Na sua representação deve ser colocado - ao lado do Z.
Z_ = {..., -3, -2, -1, 0}

- Inteiros não positivos e não – nulos
São os números inteiros do conjunto do Z_ excluindo o zero.
Na sua representação devemos colocar o _ e o * ao lado do Z.
Z*_ = {..., -3, -2, -1}

- Inteiros não negativos
São os números positivos incluindo o zero.
Na sua representação devemos colocar o + ao lado do Z.
Z + = { 0,1 ,2 ,3, 4,...}
O Conjunto Z ₊ é igual ao Conjunto dos N

- Inteiros não negativos e não - nulos
São os números do conjunto Z+, excluindo o zero.
Na sua representação devemos colocar o + e o * ao lado do Z.
Z* + = {1, 2, 3, 4,...}
O Conjunto Z* ₊ é igual ao Conjunto N*

A Formação da Identidade da Criança
Como ocorre a formação da identidade durante o primeiro ano de vida.

A importância da música no processo de ensino-aprendizagem
A relação da música com o raciocínio lógico.

A importância da parceria família e escola
Os benefícios da parceria família-escola.

A importância de planejar o estudo
Como realizar as lições de casa com sucesso.

A participação dos pais no início das aulas
O apoio dos pais é fundamental na volta às aulas.

Adiando a Decisão
Parar tudo pode ser uma opção para escolher a profissão.

Agressões na Sala de Aula
Atitudes que auxiliam professores a amenizar brigas dentro da escola.

Amigos do Fazer
Projeto social que trabalha a integração da comunidade.

Articulação da escola com a família
Uma parceria que pode gerar bons frutos.

As conseqüências de ser professor
Os danos na saúde do professor provocados pela profissão.

Atuação dos pais na educação
Como os pais podem contribuir para o desenvolvimento da criança na escola.

Avaliação Escolar
Considerações sobre a forma de se avaliar um aluno.

Boa Postura na Sala de Aula
Fatores que prejudicam a boa postura e o aprendizado.

Brincadeiras e Valores Humanos
Jogos e brincadeiras atuam na construção de um sujeito fortalecido emocionalmente.

Brincando dos Dez aos Doze Anos
Aspectos lúdicos para o desenvolvimento integral e social da faixa etária.

Brincando dos Seis aos Nove Anos
Atividades lúdicas e importantes para o desenvolvimento integral e social da criança.

Artigos de curiosidade

Bebidas Energéticas
Bebidas que estimulam o metabolismo.

A diferença entre o FBI e a CIA
Conheça a maior agência policial do mundo e o serviço de inteligência estadunidense.

A Diferença entre Psiquiatra, Psicólogo e Psicanalista
A atuação das profissões "psis".

A Doença mais Antiga do Mundo
Os primeiros regitros da doença na história.

A Eficácia do Riso
Por que as pessoas riem quando escutam uma piada?

A formação de redemoinhos
Fatores que proporcionam a formação de um redemoinho.

A história do Mario
O sucesso da série Mario e o desenvolvimento do personagem.

A Hora do Planeta (Earth Hour)
Um ato simbólico de apelo contra os problemas ambientais causados pela ação humana.

A luz do Vaga-lume
O que impulsiona as emissões luminosas do vaga-lume?

A muralha da China é visível do espaço?
A decepção dos chineses em saber que tudo não passava de um equívoco.

A Origem da Lua
Conheça as teorias sobre a origem da lua.

A Origem do Desodorante
Quando e como o desodorante foi criado.

A toque de caixa
A origem militar do termo que bem descreve o nosso cotidiano.

Aditivos de alimentos
Quais são as substâncias adicionadas nos alimentos para conservar e dar cor.

Alimentação Vegetal x Alimentação Animal
Que tipo de alimentação é mais saudável?

Aniversário
A origem do bolo de aniversário e das velas.

Artigo de fatoração de expressão algébrica

Agrupamento
Fator comum, Expressão algébrica, Termo em evidência, Fatoração, Fatoração de expressão...

Diferença de dois cubos
Fatoração, Fatoração de expressão algébrica, Expressão algébrica, Soma de dois cubos, Diferença...

Diferença de dois quadrados
Fatoração de expressão algébrica, Binômio, O que é binômio, Forma fatorada da expressão...

Fatoração: Fator Comum em Evidência
Fatorando uma expressão algébrica, fator comum em evidência.

Soma de dois cubos
Fatoração de expressão algébrica, Fatoração, Cubo, Elevado ao cubo, Soma de dois cubos,...

Trinômio do quadrado perfeito
Fatoração de expressão algébrica, Trinômio, Quadrado perfeito, Quadrado, Área do quadrado, Raiz...

Trinômio do tipo x² + Sx + P
Fatoração, Expressão algébrica, Expressão, Fatoração de expressão algébrica, Soma, produto,...

Fatoração - Oitavo ano

Existe uma forma para fatorar números, por exemplo:

Os números 32 ; 120 ; 360 podem ser fatorados em fatores primos, sendo assim temos:
32 = 2 . 2 . 2 . 2 . 2 = 25
fatores primos

120 = 2 . 2 . 2 . 3 . 5 = 23 . 3 . 5
fatores primos

360 = 2 . 2 . 2 . 3 . 3 . 5 = 23 . 32 .
fatores primos

Da mesma forma é possível fatorar expressões algébricas. A fatoração, tanto de números como de expressões algébricas, são formas diferentes de representar um número ou uma expressão algébrica. Por exemplo:

♦ O número 45 pode ser representado por uma fatoração 3² . 5, pois se resolvermos a potência e a multiplicação chegaremos ao valor 45.

♦x² – 1 é uma expressão algébrica que também pode ser representada de outra forma, basta fazer sua fatoração, ficando assim: (x + 1) (x – 1).

♦ 2x² – 2x + 2 é uma expressão algébrica, fatorada fica assim: 2(x² – x + 1).

A forma de fatorar expressões algébricas é diferente da fatoração de números inteiros, pois para cada tipo de expressão algébrica é utilizado um caso de fatoração diferente.

Esses casos são separados em:

• Fator comum (colocar o termo em evidência);
• Agrupamento;
• Trinômio do quadrado perfeito;
• Trinômio do tipo x²+ Sx +P;
• Diferença de dois quadrados;
• Soma de dois cubos;
• Diferença de dois cubos.

Minimo Multiplo Comum

MÚLTIPLO DE UM NÚMERO NATURAL

Como 24 é divisível por 3 dizemos que 24 é múltiplo de 3.
24 também é múltiplo de 1, 2, 3, 4, 6, 8, 12 e 24.

Se um número é divisível por outro, diferente de zero, então
dizemos que ele é múltiplo desse outro.

Os múltiplos de um número são calculados multiplicando-se esse número pelos números naturais.

Exemplo: os múltiplos de 7 são:
7x0 , 7x1, 7x2 , 7x3 , 7x4 , ... = 0 , 7 , 14 , 21 , 28 , ...

Observações importantes:
1) Um número tem infinitos múltiplos
2) Zero é múltiplo de qualquer número natural

MÍNIMO MÚLTIPLO COMUM (M.M.C.)

Dois ou mais números sempre têm múltiplos comuns a eles.

Vamos achar os múltiplos comuns de 4 e 6:
Múltiplos de 6: 0, 6, 12, 18, 24, 30,...
Múltiplos de 4: 0, 4, 8, 12, 16, 20, 24,...
Múltiplos comuns de 4 e 6: 0, 12, 24,...

Dentre estes múltiplos, diferentes de zero, 12 é o menor deles. Chamamos o 12 de mínimo múltiplo comum de 4 e 6.

O menor múltiplo comum de dois ou mais números, diferente de zero, é chamado de mínimo múltiplo comum desses números. Usamos a abreviação m.m.c.

CÁLCULO DO M.M.C.

Podemos calcular o m.m.c. de dois ou mais números utilizando a fatoração. Acompanhe o cálculo do m.m.c. de 12 e 30:

1º) decompomos os números em fatores primos
2º) o m.m.c. é o produto dos fatores primos comuns e não-comuns:

12 = 2 x 2 x 3
30 = 2 x 3 x 5
m.m.c (12,30) = 2 x 2 x 3 x 5

Escrevendo a fatoração dos números na forma de potência, temos:
12 = 2² x 3
30 = 2 x 3 x 5
m.m.c (12,30) = 2² x 3 x 5

O m.m.c. de dois ou mais números, quando fatorados, é o produto dos fatores
comuns e não-comuns a eles, cada um elevado ao maior expoente.

PROCESSO DA DECOMPOSIÇÃO SIMULTÂNEA

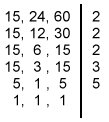
Neste processo decompomos todos os números ao mesmo tempo, num dispositivo como mostra a figura ao lado. O produto dos fatores primos que obtemos nessa decomposição é o m.m.c. desses números. Ao lado vemos o cálculo do m.m.c.(15,24,60)

Portanto, m.m.c.(15,24,60) = 2 x 2 x 2 x 3 x 5 = 120

mmc1.jpg (4787 bytes)

PROPRIEDADE DO M.M.C.

Entre os números 3, 6 e 30, o número 30 é múltiplo dos outros dois. Neste caso, 30 é o m.m.c.(3,6,30). Observe:

mmc2.jpg (2829 bytes)
m.m.c.(3,6,30) = 2 x 3 x 5 = 30

Dados dois ou mais números, se um deles é múltiplo de todos os outros, então
ele é o m.m.c. dos números dados.

Considerando os números 4 e 15, ques são primos entre si. O m.m.c.(4,15) é igual a 60, que é o produto de 4 por 15. Observe:

mmc3.jpg (2579 bytes)
m.m.c.(4,15) = 2 x 2 x 3 x 5 = 60

Dados dois números primos entre si, o m.m.c. deles é o produto desses números

Desafio

Forme o número 24 usando apenas os números 3, 3, 7, 7, uma vez cada. Você pode usar as operações +, -, *, /, e também os parênteses, se achar necessário.

Obtendo um quadrado perfeito

Você sabia que adicionando o número 1 à multiplicação de quatro números consecutivos você obtém um quadrado perfeito?

Exemplo: 1*2*3*4+1 = 25

O número dois e os proverbios

Existem diversos provérbios que envolvem o número dois. Exemplos:

"Mais vale um pássaro do que dois voando".
"Homem avisado vale por dois".
"Matar dois coelhos numa cajadada só".
"Mais vale um toma do que dois te darei".
"Dois proveitos não cabem num saco só".
"Entre os dois venha o diabo e escolha".
"Criados e bois, um ano até dois".
"Custa mais sustentar um vício do que educar dois filhos".
"Duas mudanças equivalem a um incêndio".
"Duas vezes perdido o que ao ingrato é concebido".
"Mais vale um hoje do que dois amanhã".
"Mais vale um pé do que duas muletas".
"Mais valem duas pernas do que três andas".
"Não há dois altos sem um baixo no meio".
"Dois pilotos fazem um barco ir ao fundo".
"Dois sacos vazios não se põe em pé".
"Dois sentidos não assam milho".
"Dois sobre um asno, sinal de bom amigo".
"Dois pesos e duas medidas".

Você conhece o número mágico

1089 é conhecido como o número mágico. Veja porque:

Escolha qualquer número de três algarismos distintos: por exemplo, 875.
Agora escreva este número de trás para frente e subtraia o menor do maior:
875 - 578 = 297

Agora inverta também esse resultado e faça a soma:
297 + 792 = 1089 (o número mágico)

Aviso: antes que você nos envie um e-mail dizendo que não funciona com determinados números, lembramos que devem ser usado três dígitos no cálculo. Exemplo:

574 - 475 = 099
099 + 990 = 1089

Outra forma de calcularr potencia

Pitágoras descobriu que existe outra forma de calcular potências: através da soma de números ímpares. Ele descobriu que n² é igual a soma dos n primeiros números naturais ímpares. Exemplo:
5² = 1+3+5+7+9 = 25

Presidentes da Replublica

Presidente do Brasil

Origem: Wikipédia, a enciclopédia livre.

Ir para: navegação, pesquisa

Presidente do Brasil
Pavilhão Presidencial do Brasil
No cargo Luís Inácio Lula da Silva desde 1 de janeiro de 2003
Residência	Palácio da Alvorada
Duração	4 anos, com uma reeleição consecultiva
Inaugurado por	Deodoro da Fonseca
Criado em	15 de novembro de 1889
Website	http://www.presidencia.gov.br/


República Federativa do Brasil
Este artigo é parte da série: Política e governo do Brasil

Executivo [Expandir] Presidente (Luiz Inácio Lula da Silva) Vice-Presidente (José Alencar) Casa Civil (Dilma Rousseff) Advocacia-Geral da União (José Antônio Toffoli) Ministérios Controle interno Legislativo[Expandir] Senado Federal Câmara dos Deputados Tribunal de Contas da União Judiciário[Expandir] Supremo Tribunal Federal Superior Tribunal de Justiça Tribunal Superior Eleitoral Tribunal Superior do Trabalho Superior Tribunal Militar Conselho Nacional de Justiça Federação[Expandir] Estados e Territórios Novas unidades federativas Governadores atuais Municípios (lista) Outras instituições[Expandir] Ministério Público Defensoria Pública Forças Armadas Estado brasileiro e a União Prefeitura Câmara Municipal Assembléia Legislativa Senado Estadual Presidencialismo Ordem Política[Expandir] Constituição Partidos políticos Eleições Referendos Política externa ver • disc • edite

Nota: Se procura uma lista detalhada de todos os presidentes, consulte Lista de presidentes do Brasil.

O Presidente da República é o chefe de Estado e de governo da República Federativa do Brasil. Uma vez que o sistema constitucional brasileiro optou pelo presidencialismo, o presidente da República escolhe livremente seus auxiliares diretos, os Ministros de Estado, sem interferência alguma do parlamento. De acordo com a revista norte-americana Newsweek, o ocupante do cargo é considerado como o homem mais poderoso da América Latina, devido ao status de potência regional do Brasil.^[1]

O Brasil é uma República desde 15 de novembro de 1889. O presidencialismo foi introduzido pela primeira Constituição republicana, a de 24 de fevereiro de 1891, que tomou como modelo as Constituições dos Estados Unidos e da Argentina.

O parlamentarismo republicano chegou a ser instituído no Brasil, pela emenda número 4 à Constituição de 1946, de 2 de setembro de 1961. Tratava-se de um expediente para superar grave crise política e permitir a posse do vice-presidente, João Goulart, que era acusado de ligação com os comunistas. A curta experiência parlamentarista não deu conta dos graves problemas políticos, econômicos e sociais por que passava o Brasil e, em 6 de janeiro de 1963, num plebiscito nacional, 80% dos votantes optaram pela volta do presidencialismo.

O Ato das Disposições Constitucionais Transitórias, anexo à Constituição de 1988, determinava, em seu artigo segundo, que no dia 7 de setembro de 1993 o povo brasileiro, através de plebiscito, definisse a forma (república ou monarquia) e o sistema de governo (presidencial ou parlamentar) que deveria vigorar no país. A data do plebiscito foi antecipada para 21 de abril de 1993, pela emenda constitucional número 2 de 1992. Há quem diga que tal foi feito para evitar que a realização do plebiscito na data da Independência nacional, proclamada por Dom Pedro I, predispusesse os eleitores a favor da monarquia. Em 21 de abril de 1993, data em que se comemora o republicano Tiradentes, considerado o mártir da Independência do Brasil, realizou-se o plebiscito, com expressiva maioria a favor da república presidencialista.

O atual presidente da República, desde 1 de janeiro de 2003, é Luís Inácio Lula da Silva, do Partido dos Trabalhadores (PT), eleito para seu primeiro mandato (2003-2006) por uma frente partidária composta pelo Partido Liberal (PL), Partido Comunista Brasileiro (PCB), Partido Comunista do Brasil (PCdoB) e Partido da Mobilização Nacional(PMN). Para seu segundo mandato, o presidente contou com uma coligação composta por Partido Republicano Brasileiro (PRB) e Partido Comunista do Brasil (PCdoB).

Para concorrer à Presidência, é necessário observar as limitações impostas pela Constituição:

ser brasileiro nato
ter a idade mínima de 35 anos, completos antes do pleito
ter o pleno exercício de seus direitos políticos
ser eleitor e ter domicílio eleitoral no Brasil
ser filiado a uma agremiação ou partido político
não ter substituído o atual presidente nos seis meses antes da data marcada para a eleição.

A linha sucessória é composta, em ordem, pelo vice-presidente, presidente da Câmara dos Deputados, presidente do Senado e presidente do Supremo Tribunal Federal.

O mandato do presidente da República do Brasil é de quatro anos, mas a Constituição já fixou o mandato em cinco e seis anos. Gaspar Dutra, Juscelino Kubitschek, Ernesto Geisel e José Sarney foram os presidentes que exerceram mandatos de cinco anos. O único presidente a exercer o mandato de seis anos foi João Figueiredo.

O presidente mais jovem a assumir o cargo foi Fernando Collor, aos 40 anos, em 1990. O presidente mais idoso foi Getúlio Vargas, que tomou posse aos 68 anos, em 1951. Tancredo Neves foi eleito aos 75 anos e Rodrigues Alves aos 70, mas ambos morreram antes de tomar posse.

Nove presidentes foram membros das Forças Armadas, mas desses, apenas dois chegaram ao cargo eleitos por sufrágio universal, Hermes da Fonseca, em 1910, e Eurico Gaspar Dutra, em 1946.

Apenas três presidentes exerceram o cargo por mais de um mandato: Getúlio Vargas, de 1930 a 1934, depois de 1934 a 1937, seguindo peplo Estado Novo, 1937 a 1945 e depois eleito em 1950 a 1954. Fernando Henrique Cardoso, de 1995 a 1999 e de 1999 a 2003 e Luiz Inácio Lula da Silva, de 2003 a 2007 e de 2007 aos dias atuais. Rodrigues Alves foi presidente de 1902 a 1906, e foi eleito novamente em 1918, mas como já citado, morreu antes de tomar posse..

Getúlio Vargas, durante o Governo Provisório, entre 1930 e 1934, usava o título de "Chefe do Governo Provisório" e não o de presidente da República.

O presidente do Brasil usava como gabinete de trabalho e residência o Palácio do Catete, no Rio de Janeiro, antiga capital do país. Juscelino Kubitschek morou no Palácio Laranjeiras, também no Rio e atualmente usado como residência do governador do estado.

O presidente possui ainda o Palácio Rio Negro, em Petrópolis, utilizado como residência de verão, mas o palácio está abandonado desde a era Vargas. Fernando Henrique foi o último presidente a visitá-lo, em 1997, mas não chegou a residir nele. Atualmente, o presidente utiliza o Palácio do Planalto como gabinete e reside no Palácio da Alvorada, tendo ainda a disposição a Granja do Torto, nos arredores de Brasília.

O salário atual do Presidente é de R$: 8.885.

O vice-presidente da República reside no Palácio do Jaburu, e trabalha num edifício anexo ao Palácio do Planalto.

MATEMÁTICA DA JÔ

domingo, 23 de agosto de 2009

Categoria -Cidadania

sábado, 22 de agosto de 2009

Dcumentos

Testes