quinta-feira, 30 de setembro de 2010
Desembaralhe as letras do quadro abaixo e encontre o nome de uma
figura geométrica:
________________________________________
Responda:
a) Quantas letras tem essa palavra? ___________________
b) Quantas vogais? ________________
c) Quantas consoantes? __________________
Escreva o nome de cada número no sentido horizontal do diagrama
(uma letra em cada quadradinho). No espaço em destaque na vertical
aparecerá uma palavra. Qual é?
1.
2.
3.
4.
5.
A palavra secreta é _____________________________________.
ATIVIDADES EXTRAS – MATEMÁTICA
1
2
2º ano (1ª série)
R – T – U – N – E – Â – O – L – G
quarta-feira, 22 de setembro de 2010
Não vale roubar, seja honesto(a) consigo... Porque foi descoberto que o nosso cérebro tem uma falha
Tens 1000
Acrescente 40
Acrescenta 1000
Acrescenta 30
Ainda soma outros 1000
Acrescenta 20
Acrescenta 1000 e mais 10
.
Qual é o total?
Não pode usar calculadora. tem que fazer calculo mental
quarta-feira, 15 de setembro de 2010
sexta-feira, 10 de setembro de 2010
Esse desafio é pra derreter o cérebro , vamos tentar?
Este é um desafio matemático. Dizem que os engenheiros resolvem em três minutos, os arquitectos resolvem em três horas, os médicos levam seis horas para resolver, e os advogados nunca resolvem!! 
Se és bom a matemática ou lógica, tenta resolver e escreve a resposta nos comentários ( Não expliques como chegaste lá para não dar pistas aos outros ).
Qual é o sexto número da série abaixo?
1, 2, 6, 42, 1806, ______ ?
1, 2, 6, 42, 1806, ______ ?
quinta-feira, 9 de setembro de 2010
Se fizermos algumas multiplicações descobriremos coisas interessantes
142 857 x 1 = 142 857 – é o próprio número, como todos os multiplicados por 1
142 857 x 2 = 285 714
142 857 x 3 = 428 571
142 857 x 4 = 571 428
142 857 x 5 = 714 285
142 857 x 6 = 857 142
142 857 x 7 = - deixamos em branco este resultado para que o leitor o verifique.
Entretanto, chamamos a atenção para os resultados obtidos anteriormente: todos eles são formados pelos algarismos do período da dízima, sempre na mesma ordem, mas em posições diferentes.
A beleza da Matemática
1 x 8 + 1 = 9
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 987654321
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 987654321
1 x 9 + 2 = 11
12 x 9 + 3 = 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
12345 x 9 + 6 = 111111
123456 x 9 + 7 = 1111111
1234567 x 9 + 8 = 11111111
12345678 x 9 + 9 = 111111111
123456789 x 9 +10= 1111111111
12 x 9 + 3 = 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
12345 x 9 + 6 = 111111
123456 x 9 + 7 = 1111111
1234567 x 9 + 8 = 11111111
12345678 x 9 + 9 = 111111111
123456789 x 9 +10= 1111111111
9 x 9 + 7 = 88
98 x 9 + 6 = 888
987 x 9 + 5 = 8888
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
98765432 x 9 + 0 = 888888888
98 x 9 + 6 = 888
987 x 9 + 5 = 8888
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
98765432 x 9 + 0 = 888888888
Brilhante, não é?
E que tal esta simetria:
1 x 1 = 1
11 x 11 = 121
111 x 111 = 12321
1111 x 1111 = 1234321
11111 x 11111 = 123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111 = 12345678987654321
11 x 11 = 121
111 x 111 = 12321
1111 x 1111 = 1234321
11111 x 11111 = 123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111 = 12345678987654321
Vai ai um desafio esse é facil galera
Acrescente 8 palitos a 3 palitos para obter oito.
I I I I I I I I I I I
Vamos resolver esse Sudoku
 É um tipo de quebra-cabeça que se baseia na concordância racional de números. O Sudoku é proveniente de um acrônimo da expressão “Os números devem ser únicos” (em japonês: Suuji wa dokushin ni kagiru). Continue reading ‘Sudoku – Saiba o que é’
É um tipo de quebra-cabeça que se baseia na concordância racional de números. O Sudoku é proveniente de um acrônimo da expressão “Os números devem ser únicos” (em japonês: Suuji wa dokushin ni kagiru). Continue reading ‘Sudoku – Saiba o que é’
segunda-feira, 6 de setembro de 2010
Ensino Fundamental I
Fundamentos
Prática pedagógica - Ensino Fundamental I
Cálculo mental não é chute
Professoras de Jundiaí realizam um trabalho de cálculo mental com os alunos do 3º ano e mostram que fazer “contas de cabeça” é eficaz para o aprendizado
Problemas com cálculo de tempo
Calcular a duração de eventos cotidianos é uma das habilidades fundamentais adquiridas pelas crianças
Memorização e cálculo
Veja algumas estratégias para ensinar a turma a memorizar alguns resultados que são a base para os procedimentos de cálculo
Vamos às compras
Fazer um brechó em sala de aula ajuda as crianças a estabelecer estratégias de solução de problemas no campo aditivo
EJA
Ampliando os horizontes na EJA
Na Educação de Jovens e Adultos o professor estimula que os alunos compartilhem estratégias matemáticas e dominem o cálculo mental
Da cabeça ao caderno
Encaminhar a passagem do cálculo mental para o registro é uma das tarefas essenciais na Educação de Jovens e Adultos
Professoras de Jundiaí realizam um trabalho de cálculo mental com os alunos do 3º ano e mostram que fazer “contas de cabeça” é eficaz para o aprendizado
Problemas com cálculo de tempo
Calcular a duração de eventos cotidianos é uma das habilidades fundamentais adquiridas pelas crianças
Memorização e cálculo
Veja algumas estratégias para ensinar a turma a memorizar alguns resultados que são a base para os procedimentos de cálculo
Vamos às compras
Fazer um brechó em sala de aula ajuda as crianças a estabelecer estratégias de solução de problemas no campo aditivo
EJA
Ampliando os horizontes na EJA
Na Educação de Jovens e Adultos o professor estimula que os alunos compartilhem estratégias matemáticas e dominem o cálculo mental
Da cabeça ao caderno
Encaminhar a passagem do cálculo mental para o registro é uma das tarefas essenciais na Educação de Jovens e Adultos
Calculo Mental

No ambiente escolar, o cálculo mental ainda não é tão valorizado quanto a conta armada. No entanto, um raciocínio que pode parecer desorganizado, na verdade, pode estar apoiado em propriedades das operações e do sistema de numeração e deve ser incentivado já nas séries iniciais. Para ajudar você a entender as diferentes estratégias mentais de cálculo e ensinar seus alunos a utilizá-las de forma cada vez mais eficiente, reunimos nesta página o melhor de NOVA ESCOLA sobre o tema, com reportagens, planos de aula, vídeos e jogos.
Fiquei triste
Meus queridos alunos não sei o que aconteceu com a prova do sétimo ano. Vamos estudar mais e conversar menos o resultado esta ai.
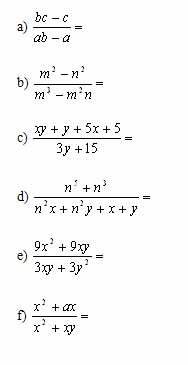
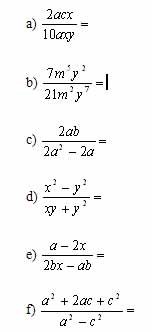
 Mover 5 palitos na figura verde para obter 3 quadrados.
Mover 5 palitos na figura verde para obter 3 quadrados.

