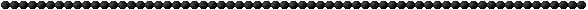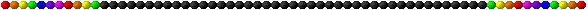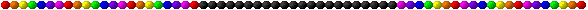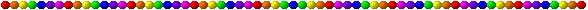Galera as avaliações serão na próxima semana

segue alguns conteúdos a serem estudados
6 * ano = numero decimal - todas as operações e multiplicações

7* ano = frações com denominadores diferentes
              as quatro operações com frações
             problemas

8  * ano = equações do 1* grau e geometria
Que tal dar uma boa estudada.

Uma curiosidade muito interessante

á faz um tempo que conheci essa brincadeira, mas nunca mais esqueci.
É o seguinte:
Se você seguir as indicações que eu passar, terei condições de ler o seu pensamento.
Pense em um número entre 1 e 9.
Multiplique por 9 o número que escolheu.
Pegue esse resultado e some os dois algarismos, um com o outro.
Do resultado dessa soma, diminua 5.
Veja a que letra do alfabeto corresponde o número que resultou dessa diminuição
Escolha rapidamente um país com essa letra.
Agora pegue a quinta letra desse país e escolha também rapidamente um animal de zoológico com essa letra.

Vou adivinhar que país e que animal você escolheu.

Desafio Matematico

Vamos quebrar a cabeça um pouco

Desafio - Essa é fácil, vamos descobrir

    Forme o número 24 usando apenas os números 3, 3, 7, 7, uma vez cada. Você pode usar as operações +, -, *, /, e também os parênteses, se achar necessário.

Esse desafio é moleza

Com seis cincos e sinais de operações, obtenha 100.

Agora eu quero ver quem vai acertar - Vamos galera vale uma viagem

Qual é o próximo número da sequência?

2, 10, 12, 16, 17, 18, 19, ....
 

Curioso esse desafio, mas vamos fazer ta

Complete a frase substituindo os traços por números que podem ser repetidos.

Se_______homem_________num bar e______ beber_____pagar, 
vem__________polícia e diz __________ prender.

Desafio

Qual é o próximo número desta sequência ?

4   8   16   32  ....

Desafio Facil

Qual é o próximo número desta sequência ?

25  20  15  10   ?

Ângulos - Retos - Agudos e Obtusos

Com relação às suas medidas, os ângulos podem ser classificados como: reto, agudo e obtuso.
 
Agudo
É um ângulo cuja medida é maior do que 0 graus e menor do que 90 graus. Abaixo temos um ângulo de 45 graus.
Reto

Um ângulo reto é um ângulo cuja medida é exatamente 90 graus. Assim os seus lados estão localizados em retas perpendiculares.Obtuso

É um ângulo cuja medida está entre 90 graus e 180 graus. Na figura abaixo temos o exemplo de um ângulo obtuso de 135 graus. O ângulo reto é provavelmente o ângulo mais importante, pois o mesmo é encontrado em inúmeras aplicações práticas, como no encontro de uma parede com o chão, os pés de uma mesa em relação ao seu tampo, caixas de papelão, esquadrias de janelas, etc...
Um ângulo de 360 graus é o ângulo que completa o círculo. Após esta volta completa este ângulo coincide com o ângulo de zero graus mas possui a grandeza de 360 graus (360 o).

Aula do prof. Marcio sobre código binário, na aula da Jô

PM Jocimar e o Proerde na aula da Jô

Simetria na Natureza

Uma das primeiras características geométricas com que deparamos quando procuramos detectá-las na Natureza é, porventura, a simetria.
A simetria na Natureza é um fenómeno único e fascinante. Esta ideia surge naturalmente ao espírito humano, remetendo-o para um equilíbrio e proporção, padrão e regularidade, harmonia e beleza, ordem e perfeição. Estes são alguns dos vocábulos que resumem reacções que temos inerentes às simetrias que abundam na Natureza, nas formas vivas e inanimadas.
Podemos encontrar simetrias sob as mais diversas formas e em diferentes locais.
Uma figura geométrica plana diz-se simétrica se for possível dividi-la por uma recta, de forma que as duas partes obtidas se possam sobrepor por dobragem. As rectas que levam a esse tipo de divisão chamam-se eixos de simetria da figura.
Um perfeito exemplo de simetria encontrada na natureza é o caso da borboleta, a qual apresenta um único eixo de simetria.


Todavia existem figuras que podem ter vários eixos de simetria ou nenhum.
A simetria bilateral é imediatamente detectada nesta imagem da cabeça de uma coruja.
No dente-de-leão é facilmente perceptível o arranjo em simetria radial.



Mas a assimetria (ou a não-simetria) é uma característica que também ocorre. Verificam-se mesmo alguns casos invulgares que têm deixado intrigados os observadores, como sucede, por exemplo, com a solha.
Notem-se, no caso do peixe achatado, os dois olhos na mesma face, assim como a boca deformada.

Podemos encontrar outras formas de assimetria, mas igualmente relacionadas com a matemática. Um das das mais frequentes, sobretudo entre as plantas, mas também presente no reino animal é a espiral, reconhecível no desenho das conchas de caracóis, búzios e afins.
É facilmente identificada, no caracol, a forma espiralada exibida pela casca.

Regularidades envolvendo hexagonos

O tema das regularidades e dos padrões, quer sejam numéricos ou geométricos, tem merecido alguma reflexão no seio deste blog. Desta vez vou conectar uma das mais importantes figuras geométricas  - o hexágono - a regularidades de natureza numérica.

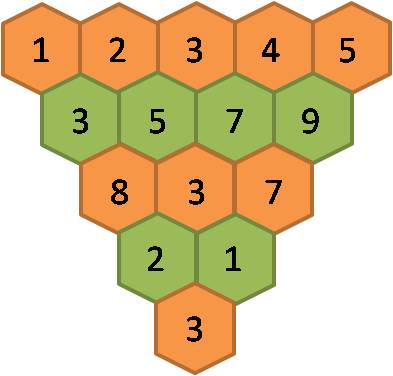
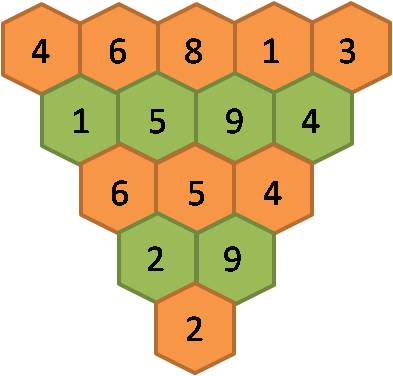
A figura seguinte, iniciada pelos primeiros cinco números naturais é construída da seguinte forma: qualquer valor numérico, exceptuando os da linha de cima, resulta da soma dos dois números que estão sobre ele na fila imediatamente acima. Quando a soma de dois desses valores ainda tem dois dígitos, estes adicionam-se e apenas o valor desta soma é colocado na figura. A título de exemplo, 5 + 7 = 12 e 1 + 2 = 3. Logo, será o valor 3 a colocar sob os valores 5 e 7:

  

 

  

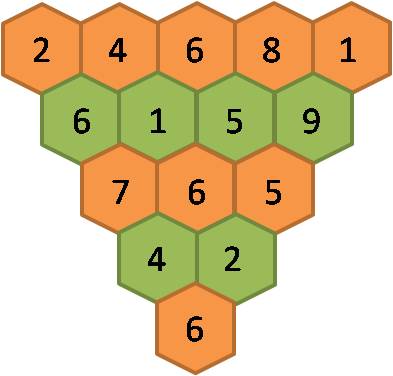
Investigar qual será o valor final se se substituírem os valores da linha de topo pelos respectivos dobros.

  

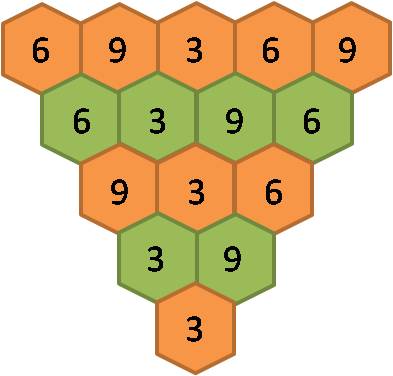
Este desafio suscita que se possa conjecturar que o valor final também será o dobro do valor final existente na figura anterior. Testemos esta conjectura:

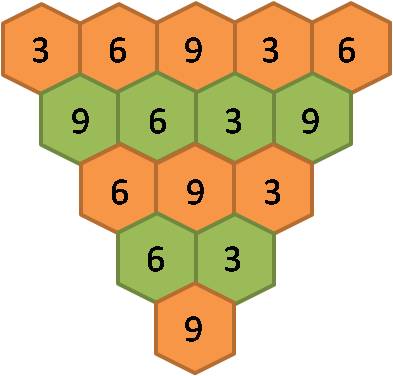
Confirma-se, pois, a estimativa acabada de fazer, o que nos leva a pensar que se a linha de topo for formada por valores que são o triplo dos respectivos valores iniciais, o valor final também será triplo do primeiro valor final. Eis a figura que confirma esta ideia:

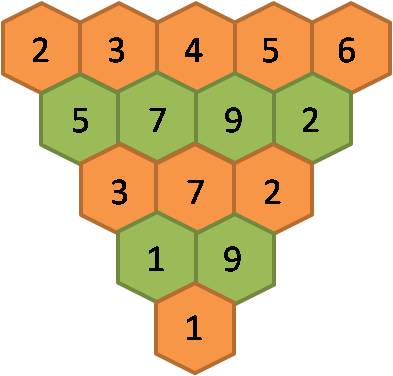
Como será o estudo semelhante para os cinco números naturais consecutivos iniciados pelo 2? E com os seus respectivos dobros e triplos também ocorrerão regularidades semelhantes a estas acabadas de verificar?

As três figuras seguintes permitem verificar-se que sim:

De facto, o valor final passou de 1 para o seu dobro (2) e para o seu triplo (3), respectivamente.

Tendo em conta a investigação acabada de realizar, explique a relação que existe entre as três figuras seguintes:

DESAFIO lOGICO

1ª fase da olimpíada brasileira
Ari, Bruna e Carlos almoçam juntos todos os dias e cada um deles pede água ou suco.

. Se Ari pede a mesma bebida que Carlos, então Bruna pede água.

. Se Ari pede uma bebida diferente dade Bruna, então Carlos pede suco.

. Se Bruna pede uma bebida diferente da de Carlos, então Ari pede água.

.Apenas um deles pede sempre a mesma bebida.

Quem pede sempre a mesma bebida e que bebida é essa?

(A) Ari; água

(B) Bruna; água

(C) Carlos; suco

(D) Ari; suco

(E) Bruna; suco

Código binário na aula da Jô

 Prof. Marcio explicando o código binário na aula da Jô - Galera do 6º Ano da Fundação Educacional de Andradina 
Assista uma parte da aula

Operações Inversas

---

Gilberto Gil, num dos versos da música Copo Vazio, lembra que um copo vazio está cheio de ar!

Se enchermos um copo de água e a seguir o esvaziarmos ele volta a ficar cheio de ar.

Responda rápido: o avesso do avesso é avesso ou é direito?

Quando uma operação desfaz outra realizada anteriormente, determinando a volta ao estado original, dizemos que uma é a inversa da outra.

Vejamos mais alguns exemplos:

A adição e a subtração são operações inversas. Uma desfaz o que a outra fez. Se a um número a somamos o número b, obtemos o número c, então de c subtraimos b, voltamos ao número a. Essa idéia pode ser representada assim:
Da mesma forma:

Entre a multiplicação e a divisão há uma relação parecida com a que existe entre a adição e a subtração. Veja os exemplos:

A multiplicação e a divisão são operações inversas. Uma desfaz o que a outra fez. Se o número a é multiplicado pelo número b, obtendo-se o número c, então, dividindo c por b voltamos ao número a.
Da mesma forma:

Em outras palavras essa idéia pode ser expressa assim: dividir o número a pelo número b significa encontrar o número c que, multiplicado por b, dá a. Assim, por exemplo, dividir 793 por 13 significa encontrar o número que multiplicado por 13 dá 793. Que número é este?

De fato, 61 x 13 = 793.

Nesse cálculo mental, a divisão de 793 por 13 foi efetuada com base na relação inversa existente entre a multiplicação e a divisão. Ela não foi efetuada assim:

Nomenclatura: quando a : b = c chamamos a de dividendo, b de divisor e c de quociente. Por exemplo, na divisão de 793 por 13, 793 é o dividendo, 13 é o divisor e 61 é o quociente

Existem diversos provérbios que envolvem o número dois

 Existem diversos provérbios que envolvem o número dois. Exemplos:
"Mais vale um pássaro do que dois voando".
"Homem avisado vale por dois".
"Matar dois coelhos numa cajadada só".
"Mais vale um toma do que dois te darei".
"Dois proveitos não cabem num saco só".
"Entre os dois venha o diabo e escolha".
"Criados e bois, um ano até dois".
"Custa mais sustentar um vício do que educar dois filhos".
"Duas mudanças equivalem a um incêndio".
"Duas vezes perdido o que ao ingrato é concebido".
"Mais vale um hoje do que dois amanhã".
"Mais vale um pé do que duas muletas".
"Mais valem duas pernas do que três andas".
"Não há dois altos sem um baixo no meio".
"Dois pilotos fazem um barco ir ao fundo".
"Dois sacos vazios não se põe em pé".
"Dois sentidos não assam milho".
"Dois sobre um asno, sinal de bom amigo".
"Dois pesos e duas medidas".

Curiosidade de um numero com 3 algarismos

Escolha um numero de três algarismos: Ex: 234 Repita este numero na frente do mesmo: 234234 Agora divida por 13: 234234 / 13 = 18018 Agora divida o resultado por 11: 18018 / 11 = 1638 Divida novamente o resultado, só que agora por 7: 1638 / 7 = 234 O resultado é igual ao numero de três algarismos que você havia escolhido: 234.

Teorema de Pitagoras

"Num triângulo retângulo o quadrado da hipotenusa éigual à soma dos quadrados dos catetos".

No geral, a demonstração do teorema de Pitágoras nos livros escolares tem um enfoque bastante algébrico: a partir de semelhança de triângulos tem-se relações de proporcionalidade e com alguma álgebra obtem-se o resultado. Vamos apresentar uma demonstração com grande apelo visual, usando conceito de área. Para isto enunciamos o teorema de forma diferente:

"Num triângulo retângulo a área do quadrado com lado igual à hipotenusaé igual a soma das áreas dos quadrados com lados iguais aos catetos".

A demonstração visual é obtida transformando-se os quadrados com lados iguais aos catetos, sucessivamente, em paralelogramos de mesma área, até chegar-se aos retângulos que compõem o quadrado com lado igual à hipotenusa, conforme a figura:

Exercícios de Equações do Primeiro Grau

Resolva as equações a seguir:

a)18x - 43 = 65

b) 23x - 16 = 14 - 17x

c) 10y - 5 (1 + y) = 3 (2y - 2) - 20

d) x(x + 4) + x(x + 2) = 2x² + 12

e) (x - 5)/10 + (1 - 2x)/5 = (3-x)/4

f) 4x (x + 6) - x² = 5x²

Devemos observar duas partes em uma equação, o 1º membro à esquerda do sinal de igual e o 2º membro à direita do sinal de igual.

Veja:

A balança está equilibrada. No prato esquerdo há um "peso" de 2Kg e duas melancias com "pesos" iguais. No prato direito há um "peso" de 14Kg. Quanto pesa cada melancia?

2 melancias + 2Kg = 14Kg

Usaremos uma letra qualquer, por exemplo x, para simbolizar o peso de cada melancia. Assim, a equação poderá ser escrita, do ponto de vista matemático, como:

2x + 2 = 14

Conteudo do segundo semestre do oitavo ano

Trabalharemos  com uma situação real e dela tiraremos algumas informações importantes. Observe a balança:

Tabuadas

12345
1x1 = 1
1x2 = 2
1x3 = 3
1x4 = 4
1x5 = 5
1x6 = 6
1x7 = 7
1x8 = 8
1x9 = 9
1x10 = 102x1 = 2
2x2 = 4
2x3 = 6
2x4 = 8
2x5 = 10
2x6 = 12
2x7 = 14
2x8 = 16
2x9 = 18
2x10 = 203x1 = 3
3x2 = 6
3x3 = 9
3x4 = 12
3x5 = 15
3x6 = 18
3x7 = 21
3x8 = 24
3x9 = 27
3x10 = 304x1 = 4
4x2 = 8
4x3 = 12
4x4 = 16
4x5 = 20
4x6 = 24
4x7 = 28
4x8 = 32
4x9 = 36
4x10 = 405x1 = 5
5x2 = 10
5x3 = 15
5x4 = 20
5x5 = 25
5x6 = 30
5x7 = 35
5x8 = 40
5x9 = 45
5x10 = 50
678910
6x1 = 6
6x2 = 12
6x3 = 18
6x4 = 24
6x5 = 30
6x6 = 36
6x7 = 42
6x8 = 48
6x9 = 54
6x10 = 607x1 = 7
7x2 = 14
7x3 = 21
7x4 = 28
7x5 = 35
7x6 = 42
7x7 = 49
7x8 = 56
7x9 = 63
7x10 = 708x1 = 8
8x2 = 16
8x3 = 24
8x4 = 32
8x5 = 40
8x6 = 48
8x7 = 56
8x8 = 64
8x9 = 72
8x10 = 809x1 = 9
9x2 = 18
9x3 = 27
9x4 = 36
9x5 = 45
9x6 = 54
9x7 = 63
9x8 = 72
9x9 = 81
9x10 = 9010x1 = 10
10x2 = 20
10x3 = 30
10x4 = 40
10x5 = 50
10x6 = 60
10x7 = 70
10x8 = 80
10x9 =  90
10x10 = 100

Vamos resolver esse soduku

Sudoku é um jogo de raciocínio e lógica. Apesar de ser bastante simples, é divertido e viciante. Basta completar cada linha, coluna e quadrado 3x3 com números de 1 a 9. Não há nenhum tipo de matemática envolvida.

Curiosidade

O ano de 1900 pertence a que século?
	Tendo em conta que o séc. I, se iniciou no ano 1 (não houve ano zero) e decorreu até ao ano 100, uma vez que um século é um período de 100 anos, devemos considerar que o séc. XIX se iniciou no ano de 1801 e terminou no ano de 1900. Desta forma, o ano de 1900 foi o último ano do séc. XIX.
O que é a amplitude de um ângulo e em que unidades se mede?
	A amplitude de um ângulo é a medida que corresponde à abertura do ângulo. A amplitiude mede-se em grau (1º = 1/360 da circunferência), em grado (1 g corresponde aproximadamente a 0,9º) ou em radiano (1 radiano é igual ao arco de uma circunferência de comprimento igual ao seu raio ).
O que é um ângulo agudo?
	Um ângulo agudo é um ângulo de amplitude maior do que 0º e menor do que 90º.
O que é um ângulo giro?
	Um ângulo giro é um ângulo cuja amplitude (medida do ângulo) é igual a 360º.