Revisão 8º Ano = Fatoração todos os casos

I - Fatore colocando em evidência


II - Fatore os trinômios quadrados perfeitos



III - Fatore as diferenças entre quadrados



IV - Fatore os trinômios de Stevin



V - Fatore as Somas ou diferenças entre dois cubos



VI - Fatore por agrupamento

Revisão 8º Ano

01. Fatorar: (a + b) . x + 2(a + b)
02. Fatorar: (x + y)2 - (x - y)2
03. Fatorar: x4 - y4
04. Fatorar: 25x2 + 70x + 49

Os caçadores de patos

Galera querida vale uma brinde quem acertar.

Dois pais e dois filhos saíram para caçar patos. Cada um deles acertou em um pato e nenhum atirou no mesmo. Entretanto somente três patos foram abatidos.

    Como isso foi possível?

Desafio Matematico

Com 24 palitos de fósforos forme 9 quadrados, como mostra o desenho. Tirando 4 fósforos, deixe 5 quadrados.

  

Galera vai mais um desafio.

Revisão do 7º Ano

Alguns exercícios do 7º ano
Complete com ,< ,> ou =
1......-3
-( -5 ) ......_ ( -9 )
3....-7
-....+18
Coloque em ordem crescente os numéros inteiros relativos
-3, 4 , -78 , 234 - 0 , -3, -7 11
123 , -87 , 890 , -56 , 34 , 0 , -1

DESAFIO LOGICO

Num sítio existem 21 bichos, entre patos e cachorros. Sendo 54 o
total de pés desses bichos, calcule a diferença entre o número
de patos e o número de cachorros.

Desafio Matematico

Ajude o sorveteiro a pensar: Com 8 números 8 e os sinais de adição (+), eu tenho que chegar ao número 1000 exato.

Desafio Matematico

Perguntaram para o senhor Enigmático quantos primos ele tinha. Ele respondeu na forma de um enigma:
"A metade deles mora em Salvador. A quarta parte mora em São Paulo. Um sétimo deles mora em Florianópolis. Restam ainda 3 primos que se mudaram para o Japão".
Quantos são os primos de Enigmático?

Galera vai alguns exemplos de fatoração para alunos de 8º

Fatore  o fator comum das expressões algébricas: a ) 2b4 – 4b² – 8b = ...................................................... b ) x² + 2x = ..................................................................... c ) a6 – 4a²= ........................................................................ d ) 5a²b³c4 + 25   abc + 50a4bc² =......................................... e ) ab + 3b – 7b =.................................................................

Fatoração por diferença de quadrados: a) a2 – 49 = ................................................................. b ) 9x2 – 16 =............................................................... c ) 5y2 – 25 =................................................................. d ) 9m2 – 36 =............................................................ e ) x2 – y2 = .................................................................

Fatore a expressão E = a2 + ba + 2a + 2b e assinale a resposta certa: a) E = (a + b) (a + 2) b) E = (a + b) (a - 2) c) E = (a - b) (a - b) d) E = (a + b) (a + b) e) E = (a + 2b) (a - 2)

Exercícios de revisão

1 – Indique com um número positivo ou negativo:

a) um lucro de R$ 90 000,00

b) um prejuízo de R$ 48 000,00

c) uma dívida de R$ 1 230,00

d) um depósito de R$ 4 580,00

2 – Qual o número que cada letra está representando?

a) a – 3 = +2

b) – 1 + y = -3

c) x – 2 = - 3

d )  5 – z = - 7

3 – Calcule :

a ) | 5 |

b) | -10|

c) - | 15 |

4 – Com a ajuda de reta numérica compare os números utilizando os sinais > ou <:

a)  - 4  e 3

b)  - 10  e 0

c) - 1000 e 5

d) – 12 e 12

5 – Escreva na forma crescente:

a) 4, -1, 5, -3, 0, 1 e -2

b) 1, -5, -10, 9, 18, -30, -20 e 8

6 – Calcule:

a) (-4) + ( +38)

b) ( - 25) + ( + 25)

c) (-715) + ( +82)

d) ( - 34) – ( -12)

e)  - 23 + 37

f) - 43 + 82

g) – 53 + 79 – 18 – 7 + 15 -  39 + 18

Divisão de números decimais

Vejamos, a divisão de números decimais também pode ser transformada em uma divisão de número inteiros, fazendo-se alguns ajustes.
Para dividirmos 17,4 por 3, por exemplo, poderemos tirar a vírgula multiplicando-se os dois números por 10. Efetuaremos, então, a divisão de 174 por 30.17,4 : 3 = 5,8

Por que foram inventadas as figuras geométricas

O homem primitivo desenhava o que sentia e o que via. Eram as chamadas pinturas rupestres, desenhos naturais, livres, que ficaram registrados em muitas cavernas em diversas regiões do mundo. Assim nasceu a chamada arte pictórica. O homem não sabia o que eram triângulos, quadrados ou hexágonos, pelo menos até sentir a necessidade de construí-los, quando passou a viver fora das cavernas. Com esta mudança teve início uma nova e importante atividade: a de construir. Inicialmente rústicas, as construções logo exigiram um aprimoramento nos traços e nas definições. O desenho tornou-se uma ferramenta básica nesse processo, aliada à valorização das formas como elemento de harmonia e beleza. Foi na Grécia que se deu um importante passo na teorização da ciência das formas.   Hoje em dia os materiais usados na construção de pontes pênseis ou de tirantes adotam formas poligonais, que dão segurança e modernidade à sua estrutura 1. Polígonos na vida cotidiana Andando pelas ruas de qualquer cidade do mundo podemos ver uma grande quantidade de formas que nos lembram os polígonos; uma placa de trânsito, um semáforo ou uma faixa de pedestres. Também em casa vemos numerosas formas poligonais nos objetos que nos cercam: nos móveis, nos utensílios de cozinha, nos pisos, nos formatos dos azulejos. 2. Elementos e classificação As linhas poligonais são formadas por segmentos da reta. As que têm suas extremidades livres são linhas poligonais abertas, e as que não têm as extremidades livres são fechadas (Figura 1).  Figura 1 Para lembrar: Polígono é a parte do plano limitada por uma linha poligonal fechada. 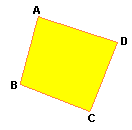Observe que o interior da linha poligonal ABCD (Figura 2) está colorido: esta linha e seu interior formam um polígono. Figura 2 O contorno do polígono é a linha poligonal fechada que o limita. Passeando pela rua, podemos observar a utilidade das figuras geométricas (retângulos) até mesmo numa faixa de pedestres Os lados desta figura geométrica são compostos pelos segmentos de reta que formam a linha poligonal. Denominamos vértices do polígono os pontos em que dois lados se unem. Figura 3a Figura 3b Os ângulos do polígono são os ângulos internos formados pelos lados do polígono (Figura 3a).  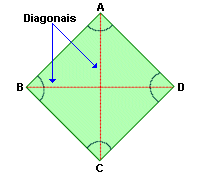As diagonais de um polígono são os segmentos que unem dois vértices não consecutivos (Figura 3b).  Se traçarmos diagonais em um polígono, podemos decompô-lo em triângulos (Figura 3b).  Os polígonos podem ser classificados segundo o número de lados que tiverem (Figura 4). Assim:  Figura 4 • Com 3 lados serão triângulos. • Com 4 lados serão quadriláteros. • Com 5 lados serão pentágonos. • Com 6 lados serão hexágonos. • Com 7 lados serão heptágonos. • Com 8 lados serão octógonos. • Com 9 lados serão eneágonos. • Com 10 lados serão decágonos. • Com 12 lados serão dodecágonos. • Com 20 lados serão icoságonos. Geralmente são nomeados indicando-se o número de lados: polígono de 13 lados, de 24 lados, e assim por diante. Para lembrar: Figura 5 Os polígonos também são classificados segundo seus ângulos. Se uma figura tiver todos os seus ângulos convexos, isto é, menores que 180°, será um polígono convexo. Se tiver pelo menos um ângulo côncavo, maior que 180°, será um polígono côncavo (Figura 5), ao lado.   Figura 6   3. Polígonos regularesObserve os polígonos da Figura 6. Todos os seus lados são iguais e todos os seus ângulos também. São, portanto, polígonos regulares.  Observe agora os polígonos da Figura 7. Eles não têm todos os lados iguais ou não têm todos os ângulos iguais. São polígonos irregulares.  Figura 7 4. Os quadriláteros Quadriláteros são polígonos com quatro lados. Observe a Figura 8. O quadrilátero A é convexo porque todos os seus ângulos são menores do que 180°. O quadrilátero B, por sua vez, é côncavo, pois um de seus ângulos tem mais de 180°.  Figura 8 Os quadriláteros convexos classificam-se em:  •  Trapezóides. • Trapézios. • Paralelogramos. Figura 9 Trapezóides são quadriláteros que não têm lados paralelos. Trapézios são quadriláteros convexos com apenas dois lados paralelos. Paralelogramos são quadriláteros convexos que têm os lados opostos paralelos (Figura 9).  Dentro do conjunto dos paralelogramos, encontramos os retângulos e os losangos.  Para lembrar: Retângulo é um quadrilátero convexo eqüiângulo, isto é, com ângulos congruentes. Figura 10 Se exercermos uma pressão sobre um dos vértices ou sobre um dos lados, o retângulo transforma-se em paralelogramo. Portanto, o retângulo é um paralelogramo particular (Figura 10).  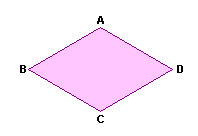Losango é um quadrilátero convexo eqüilátero, isto é, com lados congruentes.  Uma propriedade que se verifica para os paralelogramos é que as suas diagonais encontram-se no ponto médio. Figura 11 Quando essas diagonais são perpendiculares, surge a imagem do losango (Figura 11).  Para lembrar: Os retângulos e os losangos pertencem ao conjunto dos paralelogramos. Figura 12 Observe o losango: quando os ângulos são iguais (todos são ângulos retos) surge o quadrado (Figura 12).  Por isso dizemos que o quadrado é um losango particular. Também podemos chegar ao quadrado a partir de um retângulo. Basta que este tenha os lados congruentes. Nesse caso, as diagonais são iguais e cortam-se pela metade.  Figura 13 As diagonais de um retângulo quando são perpendiculares formam um quadrado (Figura 13).  Podemos dizer, então, que o quadrado é um retângulo particular.  Para lembrar: O quadrado é um quadrilátero convexo eqüilátero e eqüiângulo, isto é, tem todos os lados e todos os ângulos iguais. Figura 14 Figura 15 Os quadrados constituem a interseção dos conjuntos dos retângulos e dos losangos (Figura 14).  Agora já podemos representar o conjunto dos quadriláteros em sua totalidade (Figura 15).  5. 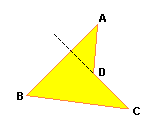Soma dos ângulos de um quadrilátero Se observarmos o quadrilátero ABCD  (Figura 16) e traçarmos uma das diagonais, esse quadrilátero fica decomposto em dois triângulos.  Figura 16 Como a soma dos ângulos internos de cada triângulo é 180°, a soma dos ângulos internos do quadrilátero ABCD  é:  180° X 2 = 360° EXERCÍCIOS 1. Completar as seis colunas da tabela da Figura 17: Figura 17 2. Num quadrilátero ABCD, Â = 90°,  = 80° e  = 70°. Quanto mede o ângulo ? 3. Qual o polígono de menor número de lados? 4. Indicar como deve ser um paralelogramo para que seja um quadrado.

Quadriláteros = Côncavos e Convexos = Contëúdo do 6º Ano

Quadrilátero

  Definição:

Quadrilátero é um polígono de quatro lados.

Quadrilátero ABCD

Em um quadrilátero, dois lados ou dois ângulos não-consecutivos são chamados opostos.

  Elementos

   Na figura abaixo, temos:

Quadrilátero ABCD

Vértices:  A, B, C, e D. Lados:  Diagonais:  Ângulos internos ou ângulos do quadrilátero ABCD: .

   Observações

1. Todo quadrilátero tem duas diagonais.
2. O perímetro de um quadrilátero ABCD é a soma das medidas de seus lados, ou seja: AB + BC + CD + DA.

   Côncavos e Convexos

    Os quadriláteros podem ser convexos ou côncavos.
    Um quadrilátero é convexo quando a reta que une dois vértices consecutivos não encontra o lado formado pelos dois outros vértices.

Quadrilátero convexo

Quadrilátero cô